The basic algorithm is this:

1. Select an arbitrary element and add it to our sorted list, S.
2. Select another arbirtrary element, x, and, using binary search, try to find x in S.
3. Place x in S according to the results of the binary search.
4. Repeat steps 2 and 3 until there are no more elements to select.

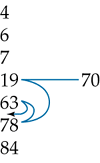
Example:

We shall show how to stick the number 70 into the already sorted list of {4,6,7,19,63,78,84} using binary search.

The following table shows the number of comparisons (worst case) to add an element to S based on the cardinality of S. This will help us get a general feel for the cost of the algorithm.

So, to sort 16 elements would require 49 comparisons. It is obvious that when n, the size of the set to sort is 2^k, where k is an element of the natural numbers, then total comparisons is given by the following summation:

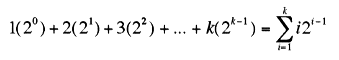
We have that when k is 1 to 5 the worst case total comparisons required to sort are 1,5, 17, 49, and 129, respectively. When examining these values, it is easy to conjecture that the series is determined by this closed form:

I could not find an example in any of the textbooks in my room to verify this; however, it is a simple proof by induction.

When k = 1, the conjecture true.
Assume true for k.

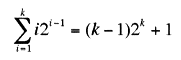
Show true for k+1:

Here we go:

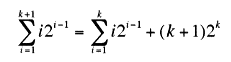
By the induction hypothesis we have that:

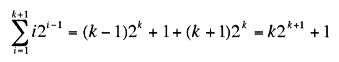
... as desired.
So, the cost for our sort is less than or equal to

What does this mean? So there is yet another sorting algoirthm that is O(nlogn). An interesting thing is it seems that if we take into account the hidden constants, the worst case for this algorithm still outperforms the average case for quicksort. Is this true?