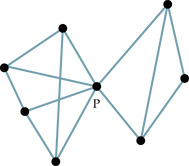
The following conjectures are new to me, but have probably been uncovered already and either credited or discredited. I have written them up for sport.

Conjecture One: Let Q be a subset of graph G - P. Let R be {G-Q-P}. If any path between arbitrary points u element of Q and v elemnt of R contains P, then we shall call P a "twist point". If a graph contains a twist point, then it does not contain a Hamiltonian cycle.
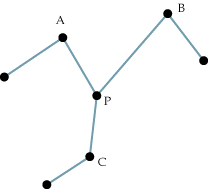
Conjecture Two: If there exists three nodes, A, B, and C, with only two edges for each node, and one edge of each node is connected to some node, P, then there does not exist a Hamiltonian cycle in the graph.
Challenge: connect any number of nodes and edges to the terminal nodes of the above graph to form a graph with a Hamiltonian cycle. If you can, then this conjecture is false.
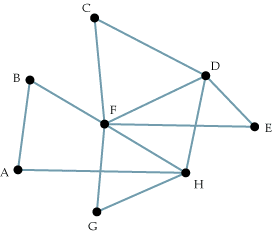
I was examining the above graph, and I drew the following adjacency matrix:
| A | B | C | D | E | F | G | H | |
| A | X | X | ||||||
| B | X | X | ||||||
| C | X | X | ||||||
| D | X | X | X | X | ||||
| E | X | X | ||||||
| F | X | X | X | X | X | X | ||
| G | X | X | ||||||
| H | X | X | X | X |
I noticed that if I drew a connection from B to C, then it would complete the two diagonals going from the top left to the lower right hand side of the matrix.
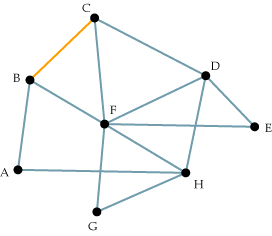
| A | B | C | D | E | F | G | H | |
| A | X | X | ||||||
| B | X | X | X | |||||
| C | X | X | X | |||||
| D | X | X | X | X | ||||
| E | X | X | ||||||
| F | X | X | X | X | X | X | ||
| G | X | X | ||||||
| H | X | X | X | X |
Noticing there existed a HC in the graph, I made the following conjecture:
Conjecture Three: If a graph contains a Hamiltonian Cycle, then the node order used to create an adjacency matrix must contain at least the following basic pattern of connections:
| . | . | . | . | . | . | . | . | |
| . | X | X | ||||||
| . | X | X | ||||||
| . | X | X | ||||||
| . | X | X | ||||||
| . | X | X | ||||||
| . | X | X | ||||||
| . | X | X | ||||||
| . | X | X |
Now, if we could only devise a method to arrange nodes to create such a pattern in polynomial time...